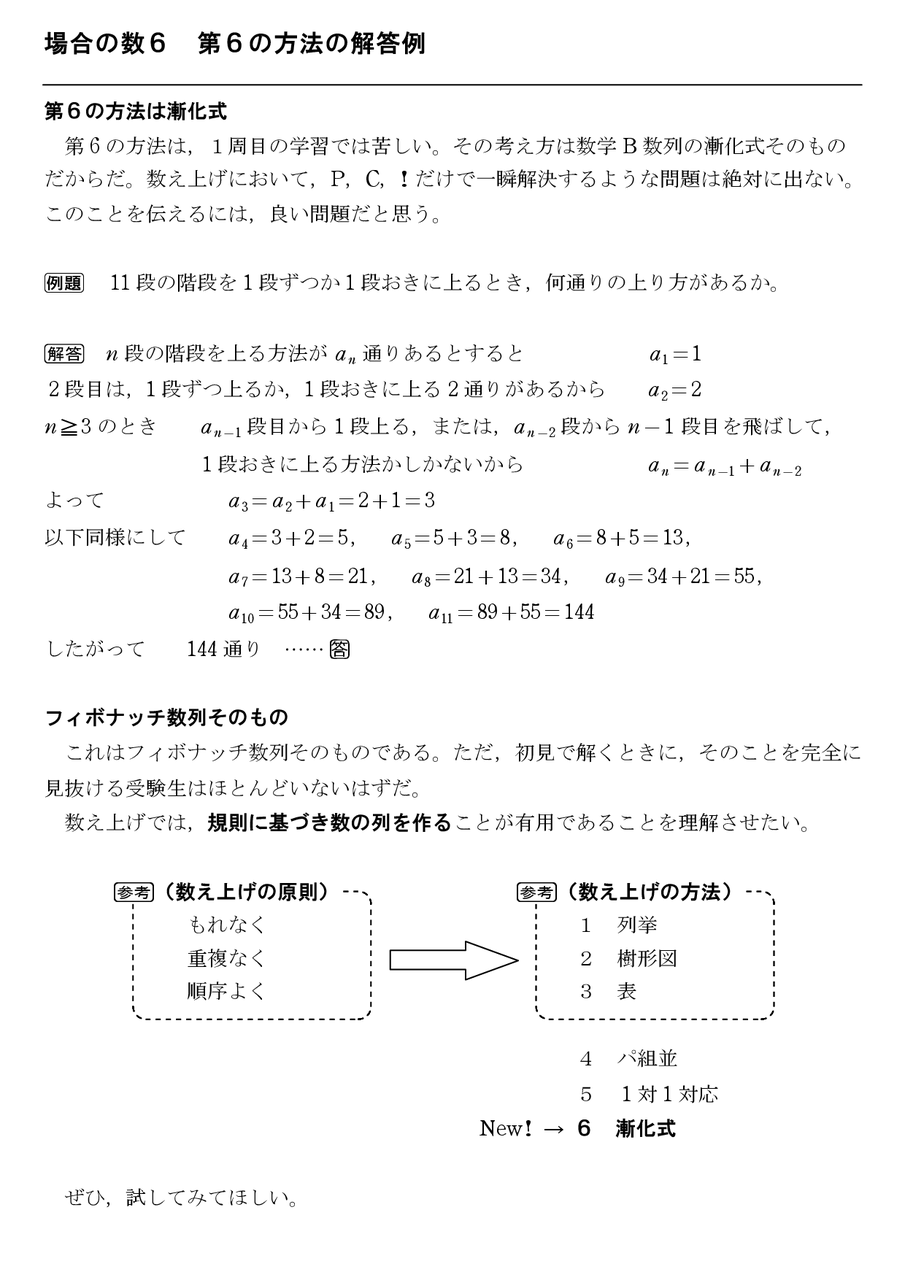
· シローの定理 適用例 巡回群の位数位数 n の群は巡回群に限るような正の整数 n がある。たとえば n = 15 がそのような数であることがシローの定理を用いることでわかる。ここで n3 5 かレストラン シロー/shiro (藤沢/洋食)の店舗情報は食べログでチェック!藤沢駅南口から徒歩5分創作オムライスやパスタをメインに様々な洋食をご提供♪ 禁煙 / 飲み放題あり口コミや評価、写真など、ユーザーによるリアルな情報が満載です!地図や料理メニューなどの詳細情報も充実。シローの定理は,群の位数と部分群に関する,次のような定理です. theorem 群 の位数が,素数 によって と,一意的に素因数分解されるとき,位数が となる部分群が少なくとも一つは存在する.

ヤフオク 01 群論 上巻 鈴木通夫 現代数学18 岩波書店 19
シロー の 定理
シロー の 定理-シローの定理 数学、とくに有限群論において、シローの定理 (Sylow theorems) は、ノルウェーの数学者ルートヴィヒ・シロー (Ludwig Sylow) (1872) にちなんで名づけられている定理の集まりであり、与えられた有限群がもつ固定された位数の部分群の個数についての詳細な情報を与える。 シローの定理は有限群論の基本的な部分をなし、有限単純群の分類における非常に重要殺菌・消毒剤 「ポンシロール」 高い有効塩素量と優れた溶解性で、安定した消毒効果と作業効率の向上を実現します。 塩素臭気が50%低減。 (当社従来品比) 車内や作業中の臭気や周辺機器材への影響を低減します。 有効塩素量や溶解度などの品質は




Algebra I Lecture Note
対象商品 シローの定理 (大学数学スポットライト・シリーズ) 佐藤 隆夫 単行本 ¥2,640 この商品は、Amazoncojpが販売および発送します。 通常配送無料(一部の商品・注文方法等を除く) 詳細 線形代数入門 森山 洋一 単行本 ¥2,4 残り2点(入荷予定あり) この商品は、Amazoncojpが販売および発送します。 通常配送無料(一部の商品・注文方法等を除く) 詳細→コーシーの剰 余項に戻る →総目次 (証明) ポイント:ラグランジュ剰余項と異なった剰余項が導出される秘密は、関数g(x)の設定でのR n の係数の違いにある。 関数f(x) が閉区間a,bで(n-1)階まで連続な導関数をもち、開区間(a,b)でn階微分可能とする。アローの定理の思想史上のインパクトについてはこれを参照。 Geoffrey Brennan, `The contribution of economics', in Robert E Goodin and Philip Pettit ed, A Companion to Contemporary Political Philosophy, Oxford Blackwell, 1993,
3100 · シローの定理とは シローの定理とはシローさんが発見した有限群論の定理たちの総称です その中で僕が一番好きなのは $p_i\in \mathbb{P}$とする$ G=p_{1}^{e_1}p_{2}^{e_2}\cdots p_{k}^{e_k}$であるとき 位数$p_{i}^{e_i}$である部分群が存在する という存在定理ですシローの定理 佐藤隆夫(数学) 本の購入は楽天ブックスで。全品送料無料!購入毎に「楽天ポイント」が貯まってお得!みんなのレビュー・感想も満載。シローの定理証明&応用 この記事では, シローの定理(Sylow theorems)の証明&応用について解説します。 シローの定理の証明 シローの第1定理 定理 $p$ が素数で, $G$ が $p^a$ で割り切れるならば, $G$ は位数 $p^a$ の部分群をもつ 証明 証明
De nieuwste tweets van @edogawamsrウイニングポスト9 オンライン対戦 最速で1000万ポイントに到達 ウイニングポスト9無印PC版とPS4版馬主ランク1位 ダビつくオンライン公式大会数学、とくに有限群論において、シローの定理 (Sylow theorems) は、ノルウェーの数学者 ルートヴィヒ・シロー (Ludwig Sylow) にちなんで名づけられている定理の集まりであり、与えられた有限群がもつ固定された位数の部分群の個数についての詳細な情報を与える。




Ntmrの数学メモ




こめ ここまで大学の講義で言えば6コマくらいか この教科書がだいたいシローの定理までやって終わる構成だけど これで大学の講義半期分くらいっぽい で これ母校で言えば2年生の下期くらいからやるんじゃないか 数学科やばい
3.シローの定理 31.群の集合への作用 本節では、シローの定理の準備として、"群の集合への作用"という概念を説明する。これはそれ自体独立し た概念であり、応用範囲が広く、その具体的事例のひとつがシローの定理である。 群の集合への作用 · の位数が であるときを考える.このとき,位数 の の部分群( 部分群という)は必ず存在する(定理4).Sylowの定理(定理7)は,位数が の部分群(このような部分群を の Sylow群という)についての定理である.Sylowの定理は有限群を考える上で基本的なものである.The Sylow theorems are a powerful statement about the structure of groups in general, but is also powerful in applications of finite group theory This is because they give a method for using the prime decomposition of the cardinality of a finite group G {\displaystyle G} to give statements about the structure of its subgroups essentially, it




Algebra I Lecture Note




位数6の群の分類 Tsujimotterのノートブック
ベルヌーイの定理は以下の式となります。 この式を簡単に説明すると、 「 流体の速度が増加すると圧力が下がること 」 を示しています。 これを身近な例でご説明いたします。 例えば、の用紙を図のように持って、息を吐きかけると、どちらに用紙が余弦定理 余弦定理とはとある三角形ABCがあるときに成り立つ の公式のことを言います。 この定理が本当になりたつのか、例をとって証明してみましょう。ここでは、 の式を証明します。 cosAの値は、Aの角度が鋭角、直角、鈍角 · シローの定理から位数 G p = q n(n − 1)/2 のシロー p部分群 U が存在する。たとえば n = 3 のとき = {() ,,}




群論序説 星 明考 本 通販 Amazon



Proof Sample Of Hierarchical Style
ST U G ~qMloM `hUz lqfw w b \qUpV b¢ Z`oV `h£{ w ¯q`oxÍw Ot QoSV ` OY¬ gz z gqx 32 33 Chapter1 y æ gÜ 1 1 } 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7x ¢ £ qzy ww «pb{ rT ? · シローの定理 (大学数学スポットライト・シリーズ)/佐藤 隆夫/矢部 博/伊藤 浩行/大矢 雅則/眞田 克典/立川 篤/新妻 弘/古谷 賢朗/宮岡 悦良/宮島 静雄(自然科学・環境) シローの定理にスポットライトを当てたテキスト。群の定義や諸性質をはじめ、部分群に関する性質、群論で最も大切



9 Sylow定理 隔壁小王的睡前故事 微信公众号文章阅读 Wemp



E G A Imp Street Two Two Pair Of Control 70 81 車 Lower Arm F Body For カスタム Qa1 パーツコントロールアーム 524 Of Gm Kit パーツ Use
De nieuwste tweets van @manetoku19112 留数定理 115 112 留数定理 定義:留数 関数f(z) が領域Dでz= z0 を除いて正則な1価関数であるとき,領域 Dの内部にあってz0 を内部に含む区分的になめらかなJourdan 曲線Cをとれば,積分 1 2πi C f(z)dz の値は曲線C のとりかたによらない。 この値を関数f(z) の点z0 における留数とい定理8 (オイラーの定理)自然数n と互いに素である自然数a について, aφ(n) · 1 ( mod n) が成り立つ. 証明 n 以下の自然数でn と互いに素な数を r1,r2,r3,¢¢¢ ,rφ(n) (1) と表す.これらに,n と互いに素である自然数a をかけた数, ar1,ar2,ar3,¢¢¢ ,arφ(n) (2) 4/12



Proof Sample Of Hierarchical Style




シローの定理 の新着タグ記事一覧 Note つくる つながる とどける
· 質問者: ゆーたんまん 質問日時: 1256 回答数: 1 件 p:奇素数とする。 G=2pならばGは巡回群もしくは二面体群となることを示せ。 シロー2部分群とシローp部分群が存在して シローp部分群が正規部分群になるというところまで分かりました。 しかし、シロー2部分群がどうなるか分からなくて詰まってしまっています。 わかる方どなたかお力を · シロー ト統計学講座 第5回 前回は「中心極限定理と標準化」について説明しました。今回はいよいよ標本から母平均の区間推定を行います。まずは母分散が既知の場合の区間推定でシロー化学株式会社, 東京都 調布市 35 likes · 2 were here 化粧品、医薬部外品の製造販売 オリジナル化粧品、トイレタリー製品受託 製造いたします。小ロット対応、お気軽に お尋ね下さい。




あすたーいずむ はい この定理は シローさんが発見したから Sylow の定理と呼ばれてる らしいです じゃ 白紙プリント配るので証明しといてね




位数p 2の群は可換である 代数学のessence 群論 Youtube
正切定理发展 编辑 法兰西斯·韦达 (Franccedil ois Viète)曾在他对三角法研究的第一本著作《应用于三角形的数学法则》中提出正切定理。 现代的中学课本已经甚少提及,例如由于中华人民共和国曾经对前苏联和其教育学的批判,在1966年至1977年间曾经将正切定理 · センター試験で毎年必ず出題される図形問題。 基本的な定理を理解していることは前提とした問題ばかりで、苦手意識を持っている人も多いでしょう。 ですが、逆に言えば、図形の基本定理を1つ1つ潰していけば、センターの図形問題は確実な得点源になってくれるのです。




位数5593の群は巡回群である 代数学のessence演習 群論 Youtube




File Labeled Triangle Reflections Svg Wikipedia




ゴリラ 原田耕一郎 群の概念が抽象的すぎる 数学セミナー17 06より 4問とはラグランジュの定理 コーシーの定理 有限アーベル群の基本定理 シローの定理の証明 何か難しいことを自分のものにするってことは それを頭の中だけであれこれイジったり




Amazon Fr 代数学 1 群と環 大学数学の入門 Toshiyuki Katsura Livres




書籍紹介詳細ページ




ヤフオク 01 群論 上巻 鈴木通夫 現代数学18 岩波書店 19



Proof Sample Of Hierarchical Style



Category 代数学の定理 Page 1 Japaneseclass Jp




Category 代数学の定理 Page 1 Japaneseclass Jp
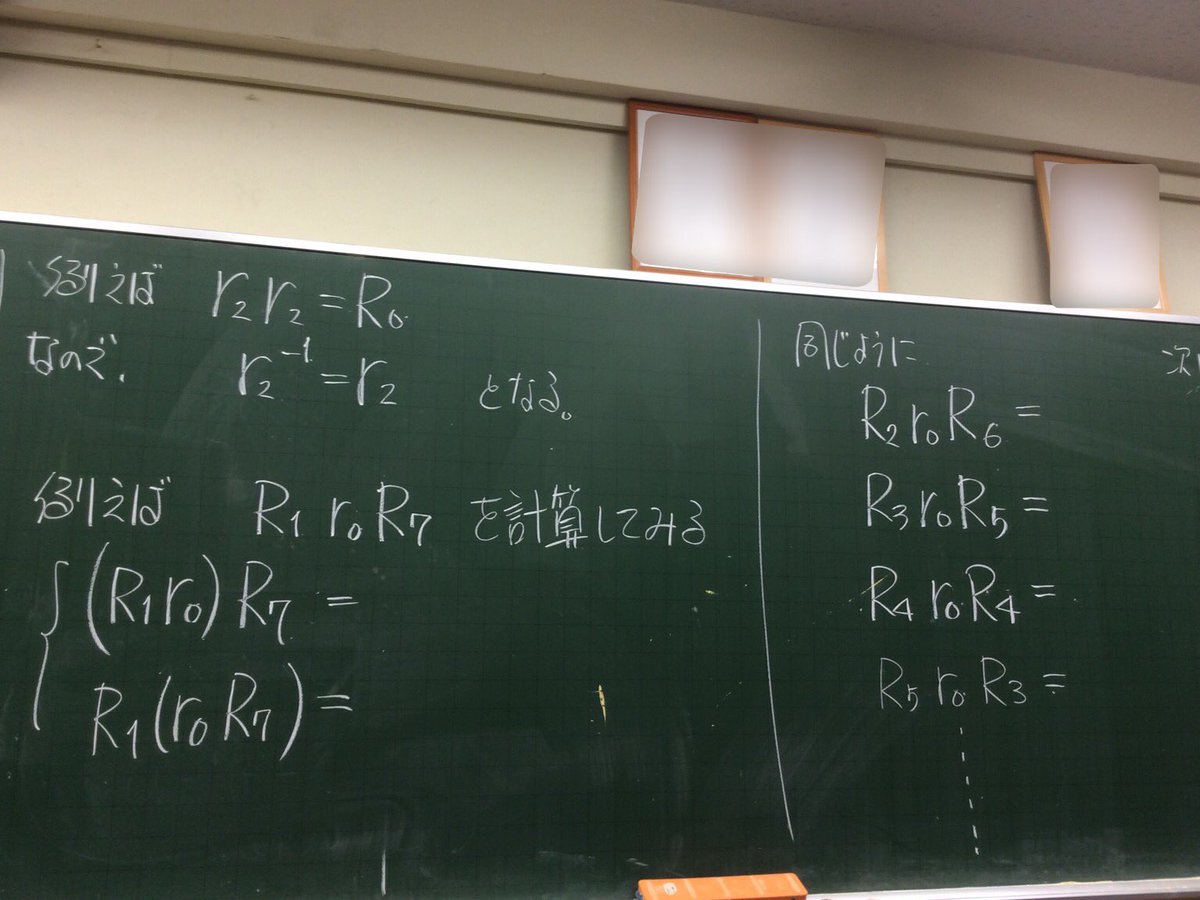



あすたーいずむ はい この定理は シローさんが発見したから Sylow の定理と呼ばれてる らしいです じゃ 白紙プリント配るので証明しといてね




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon



9 Sylow定理 隔壁小王的睡前故事 微信公众号文章阅读 Wemp



Sylowの定理 の新着タグ記事一覧 Note つくる つながる とどける




Category 代数学の定理 Page 1 Japaneseclass Jp




ヤフオク 01 群論 上巻 鈴木通夫 現代数学18 岩波書店 19




4 群作用 ノリの悪い日記




Algebra I Lecture Note




シローの定理 大学数学スポットライトシリーズ1 佐藤 隆夫 楽天kobo 日本




あすたーいずむ はい この定理は シローさんが発見したから Sylow の定理と呼ばれてる らしいです じゃ 白紙プリント配るので証明しといてね




Sylowの定理hashtag




Algebra I Lecture Note




数学の勉強の記録をブログに残す事にした おとなぱすた




Algebra I Lecture Note




Algebra I Lecture Note




群論 位数30の群の分類 龍孫江の数学日誌




Algebra I Lecture Note




群論 シロー部分群の数 Youtube




代数学 26 シローの定理 Youtube




群論 正規部分群のシロー部分群 龍孫江の数学日誌 別館の案内所




シローの定理 大学数学スポットライト シリーズ 佐藤 隆夫 本 通販 Amazon




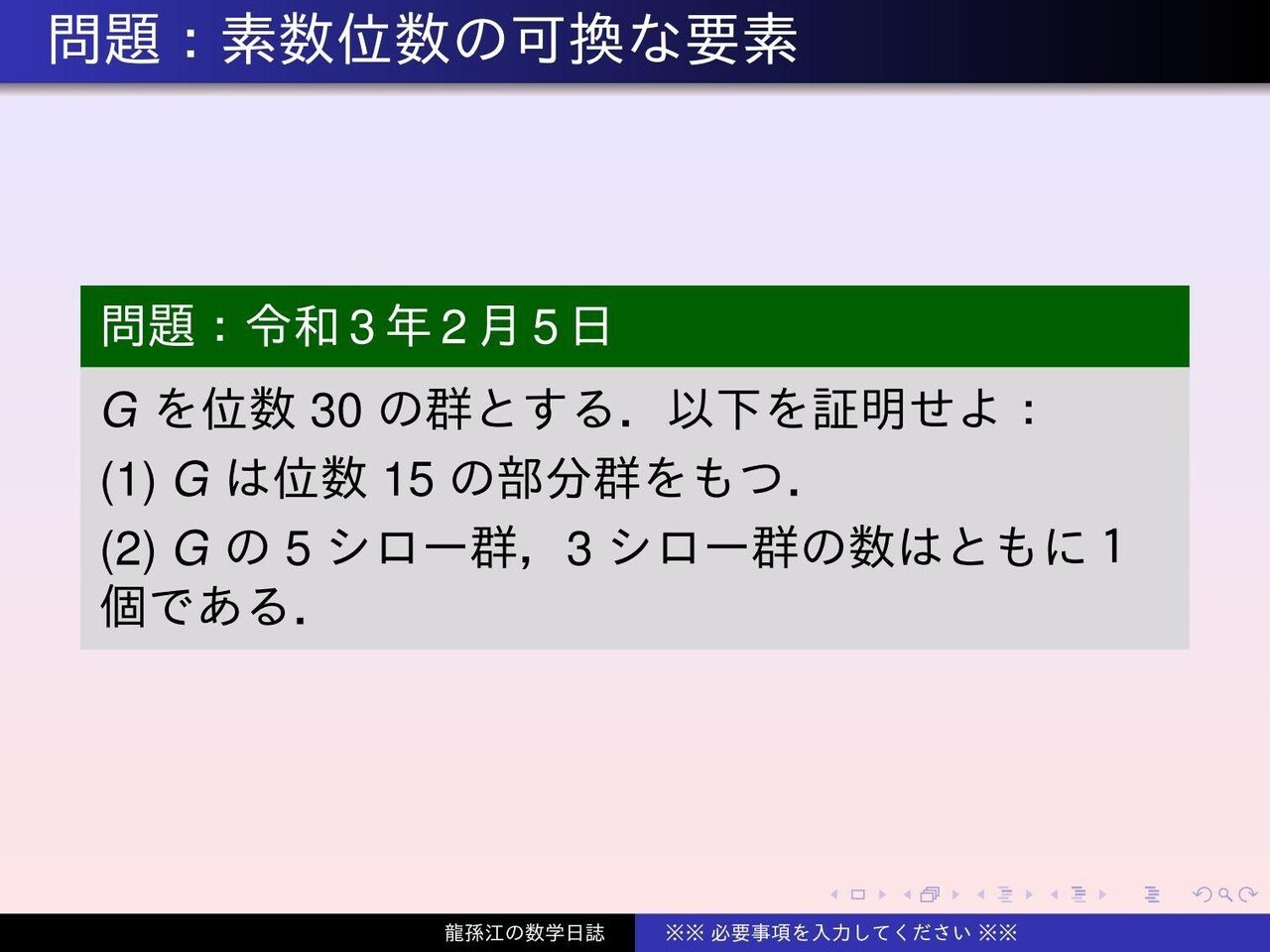
群論 素数位数の可換な要素 龍孫江の数学日誌
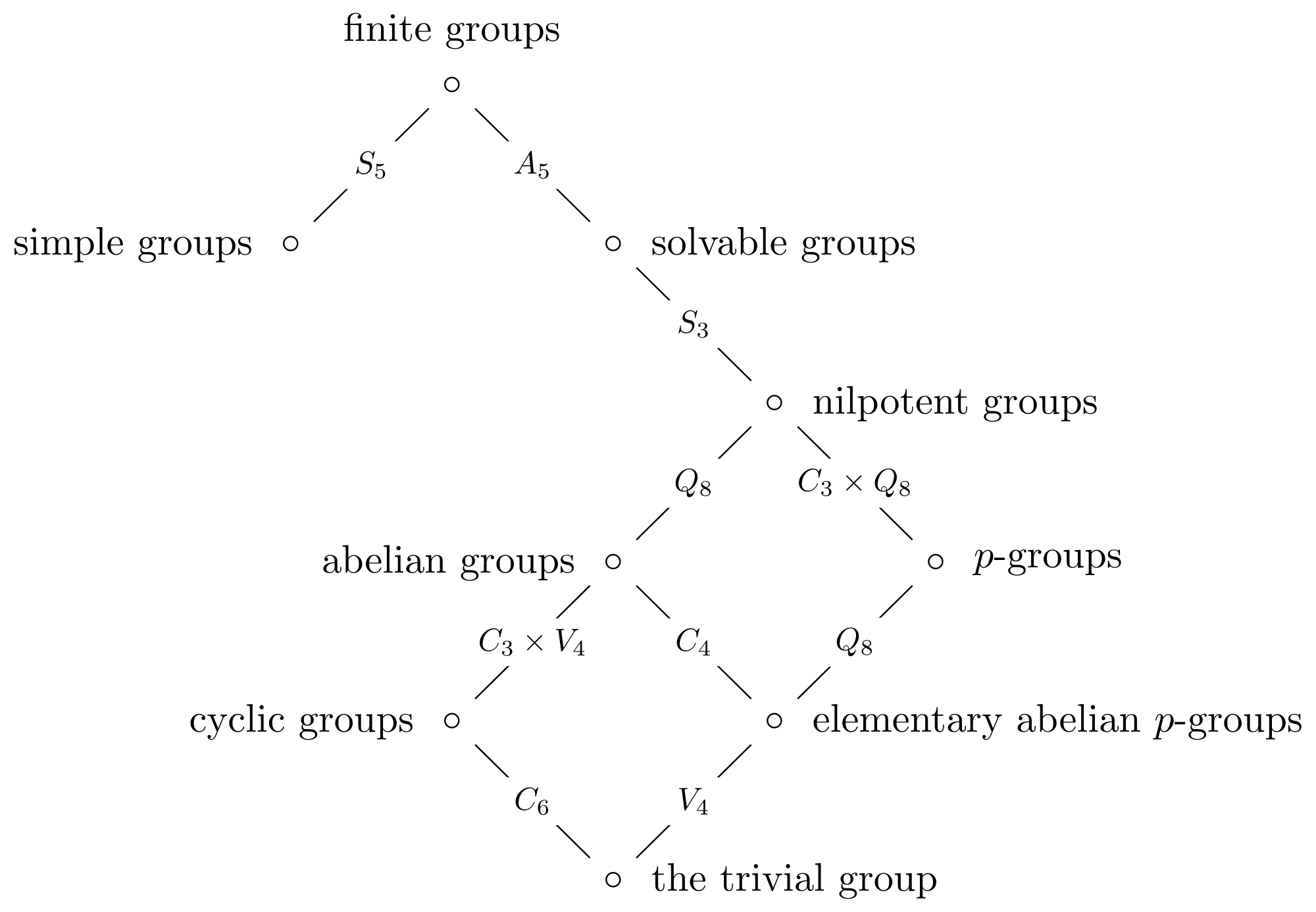



可解群 Wikipedia




Pdf The Principal 2 Blocks Of Finite Groups With Abelian Sylow 2 Subgroups
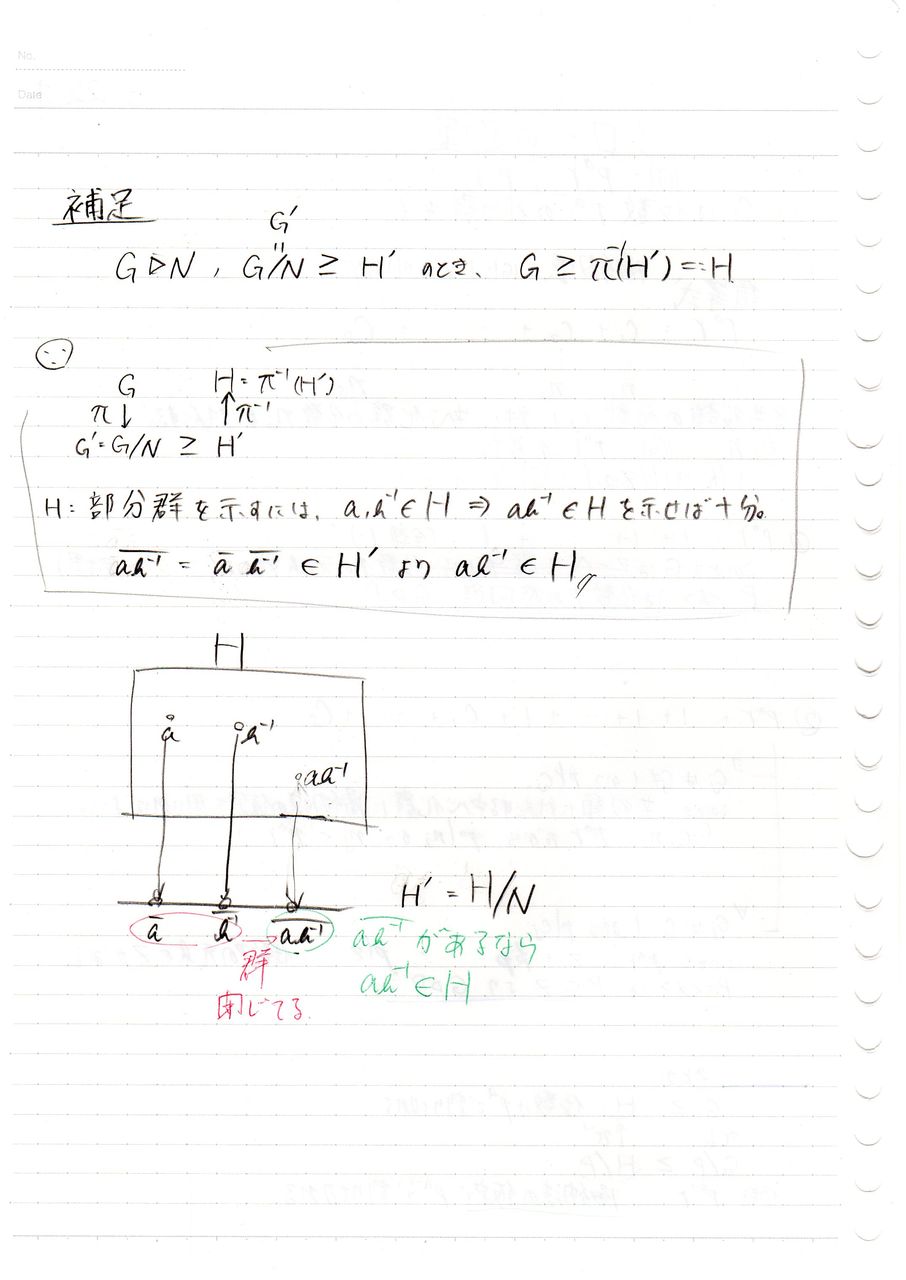



シローの定理 数学ノート置き場




今度こそわかるガロア理論 今度こそわかるシリーズ 芳沢 光雄 本 通販 Amazon




群論 シロー部分群は存在します Youtube




群論




数学日誌 In Note令和元年11月第3週分 継続購読版 龍孫江 りゅうそんこう 可換環論botオペレーター Note




ヤフオク 01 群論 上巻 鈴木通夫 現代数学18 岩波書店 19



第二章sylow 定理




Algebra I Lecture Note




ラグランジュの定理 具体例で学ぶ代数学 群論 No 14 Youtube




書籍紹介詳細ページ




Images Of ガロア理論の基本定理 Japaneseclass Jp



Proof Sample Of Hierarchical Style




シローの定理 数学ノート置き場




シローの定理 数学ノート置き場




巡回群 Wikipedia




群論 素数位数の要素と群の巡回性 Youtube




西罗定理 知乎




如何证明sylow 定理 知乎




ヤフオク 01 群論 上巻 鈴木通夫 現代数学18 岩波書店 19




シローの定理 数学ノート置き場




群論 6次対称群のシロー部分群 Youtube



0 件のコメント:
コメントを投稿